微流控纸基分析设备(μPAD)作为便携式即时检测(POCT)工具,在资源匮乏地区的早期疾病诊断和健康监测方面展现出巨大潜力。纸张具有毛细管驱动流动、多孔结构、亲水官能团、生物可降解性、成本效益和柔性等诸多优势,是微流控装置基材的理想选择。现有微流控纸基分析装置主要包括一维横向流动分析装置(1D LFA)、二维微流控纸基分析装置(2D μPAD)和3D μPAD,它们各自具备独特的结构和功能,以满足不同的检测需求。

近期,陕西科技大学蒋学教授发表综述,主要讨论了多维纸基微流控分析设备的设计策略及其在无创即时检测应用中的最新进展。此外,还深入探究了纸张内毛细驱动流动的替代理论模型,旨在为多维纸基微流控设备的基材开发和通道设计提供理论指导。相关研究成果以“Multi-dimensional microfluidic paper-based analytical devices (μPADs) for noninvasive testing: A review of structural design and applications”为题目发表于期刊《Analytica Chimica Acta》。
本文要点:
1、本文综述了与多维微流控纸基设备中的纸张基材、设计策略和检测方法相关的关键信息。
2、探讨了微流控纸基设备在无创检测中的潜在应用,包括临床诊断、生理监测和毒理学筛查等。
3、深入探究了纸张内毛细驱动流动的替代理论模型,旨在为多维纸基微流控设备的基材开发和通道设计提供理论指导。
4、批判性地讨论了多维微流控纸基设备在推进无创早期诊断和健康监测方面的未来发展潜能以及所面临的挑战。
5、多维μPAD技术的进步为提高医疗保健效率和质量提供了新的解决方案,对于改善患者护理具有重要意义。
一张图读懂全文:
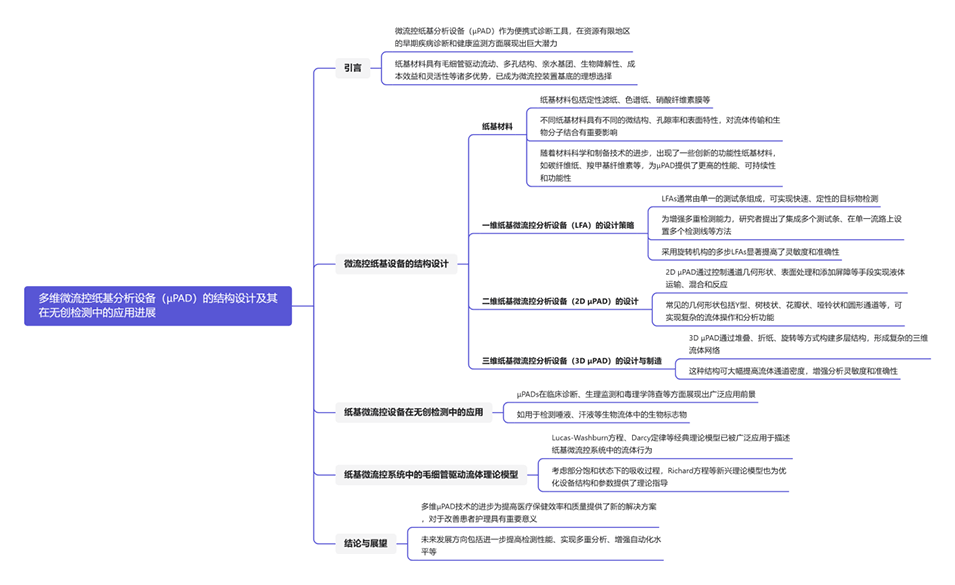
使用纸张作为微流控设备基材的主要优势包括:
1、毛细驱动流动:纸张的多孔结构和亲水性质有助于实现毛细驱动的流体输送,消除了对外部泵或电源的需求。
2、灵活性和便携性:基于纸张的设备轻便灵活、便于携带,适合于即时检测和现场应用。
3、成本效益:纸张材料价格低廉且容易获取,为制造低成本的微流控设备创造了条件。
4、生物可降解性:纸基设备可以通过焚烧等方式轻松处理,具有环境友好性。
5、易于修饰:纸张表面可以方便地进行化学或物理修饰,比如添加疏水屏障,以实现精确的流体操控。
6、生物相容性:纸张是一种生物相容材料,适用于与生物样本和分析物接触的应用。
7、符合REASSURED标准:纸基微流控设备符合世界卫生组织提出的关于POCT的REASSURED标准,包括实时通信、样本采集便携、经济实惠、灵敏度高、特异性好、操作简单、快速并可重复、无需仪器和易获取。
微流控纸基设备在无创检测中的一些潜在应用包括:
1、病毒检测:快速筛查和识别人类唾液样本中的病毒,例如SARS-CoV-2、流感病毒和HIV等。
2、代谢物和激素检测:用于检测唾液、汗液和尿液等非侵入性生物流体中的各种代谢物(如葡萄糖)和激素(如皮质醇和尿酸)。
3、电解质和生物标志物分析:同时测定尿液和汗液样本中的多种电解质(如钠和钾离子)和其他重要的生物标志物。
4、妊娠和生育测试:通过检测尿液中的人绒毛膜促性腺激素(hCG)水平来进行妊娠测试。
5、即时检测和可穿戴应用:结合智能手机和可穿戴设备,实现对生物流体中生理参数和生物标志物的实时、连续监测。
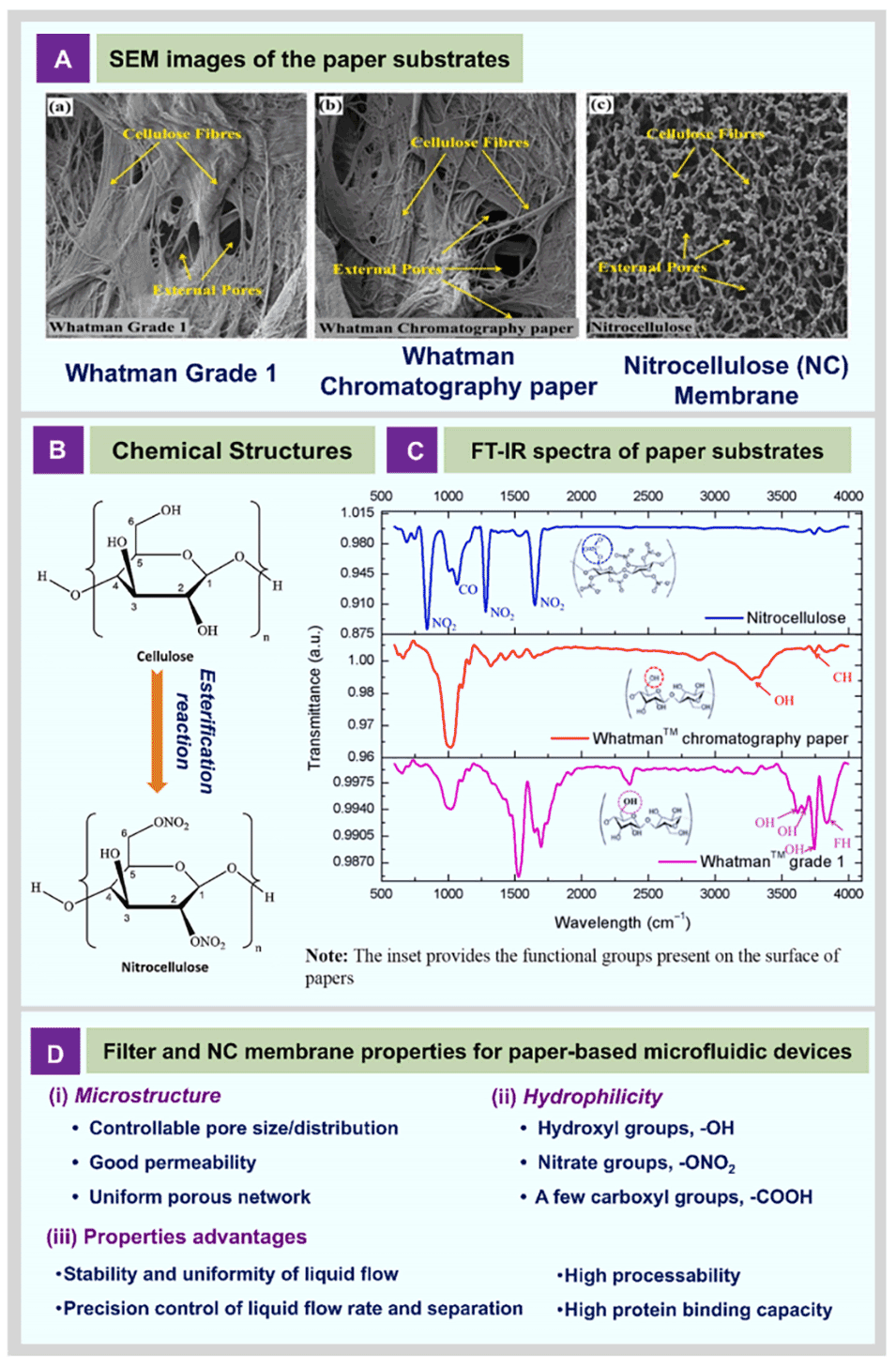
图1.(A)纤维素和硝化纤维素的化学结构;(B)纸质基材的傅里叶变换红外光谱;(C)典型常用纸质基材的SEM图像,(a)Whatman 1级定性滤纸,(b)Whatman色谱纸,(c)硝化纤维素膜;(D)用于微流控纸基设备的滤纸和NC膜的特性。
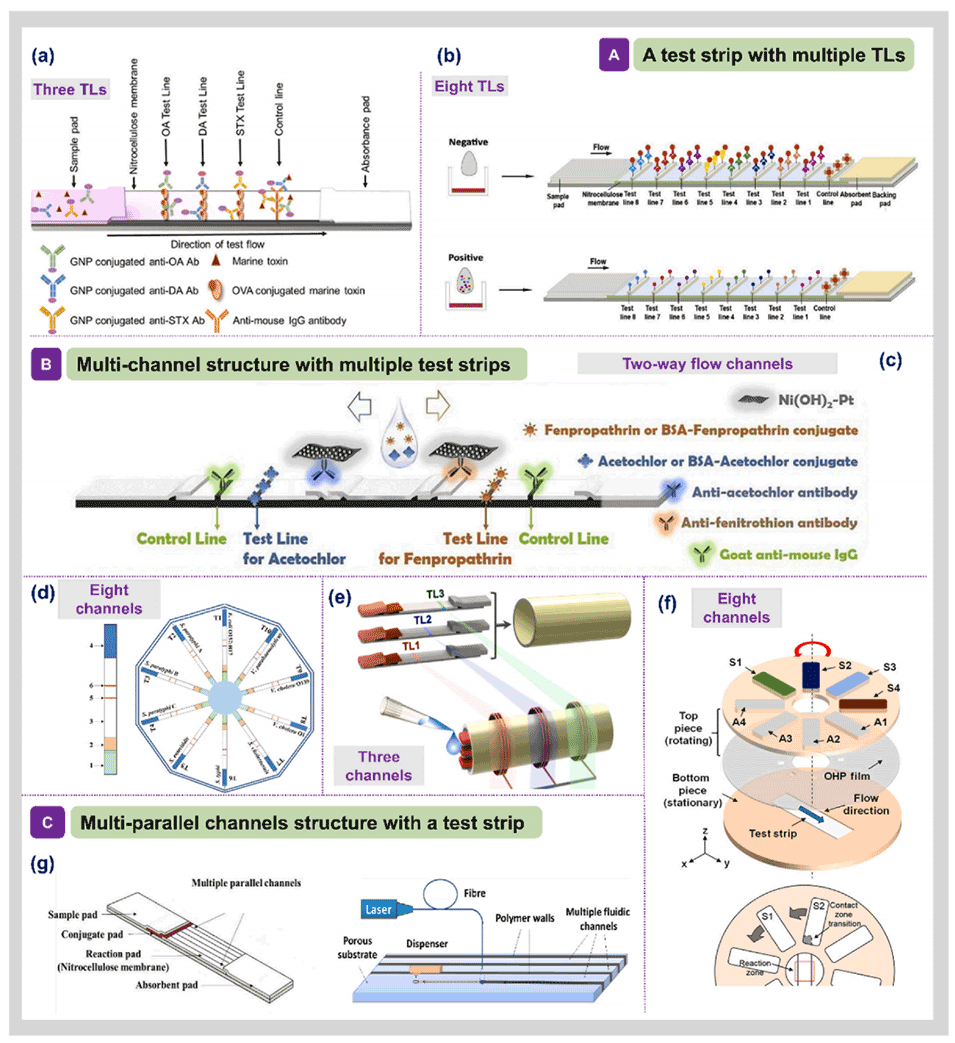
图2.多路LFA的设计策略。
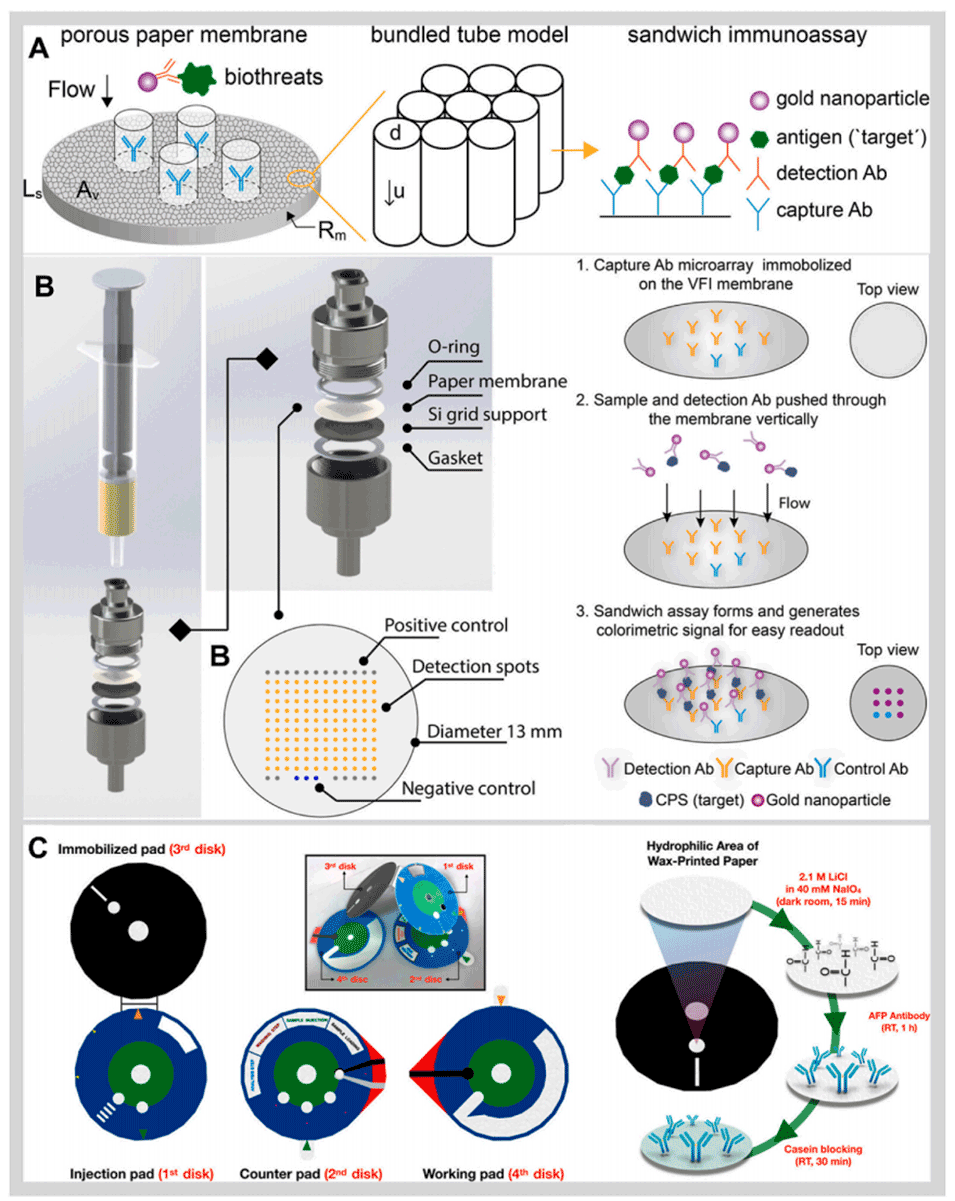
图3.(A)垂直流式纸基免疫测定原理;(B)垂直流动分析(VFA)系统方案及其工作原理;(C)纸基旋转式垂直流动分析(VFA)的结构和机理。
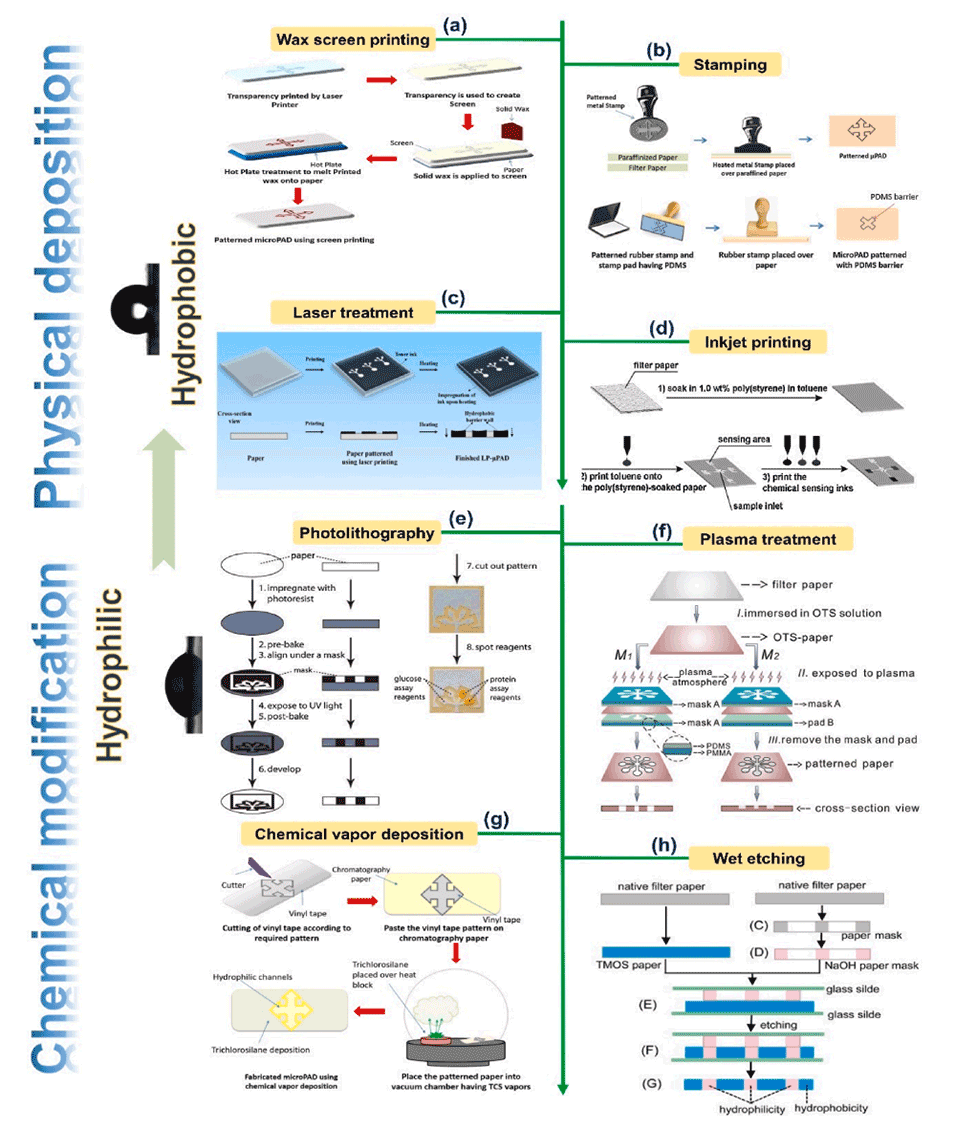
图4.μPAD的疏水屏障图案化方法概述。
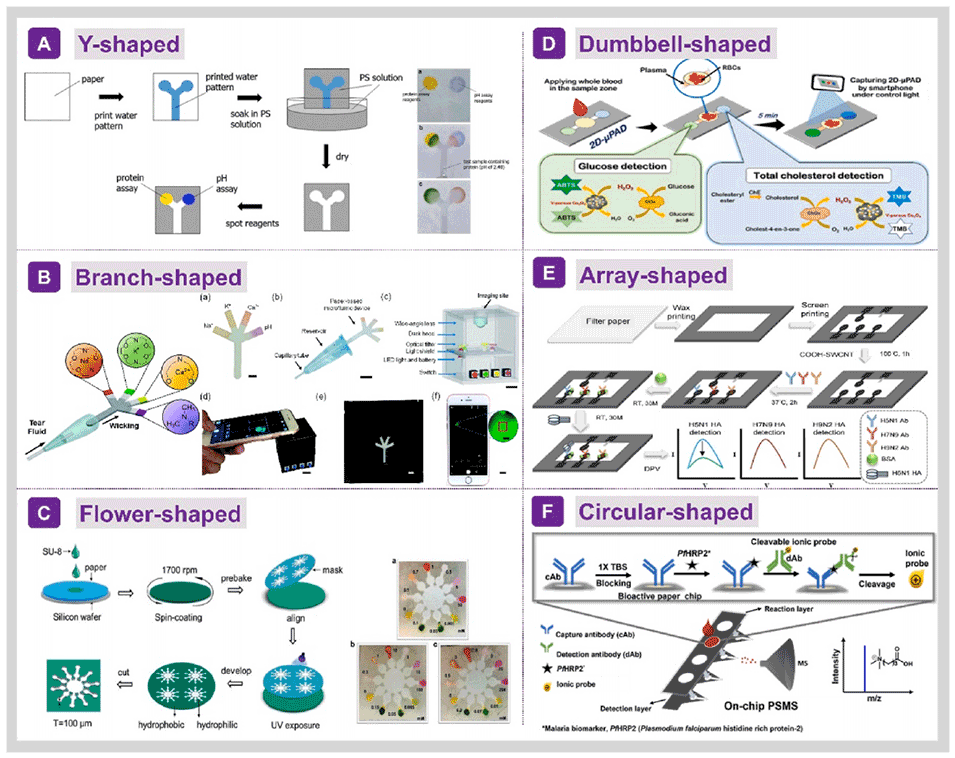
图5.2D μPAD的几何形状设计策略。
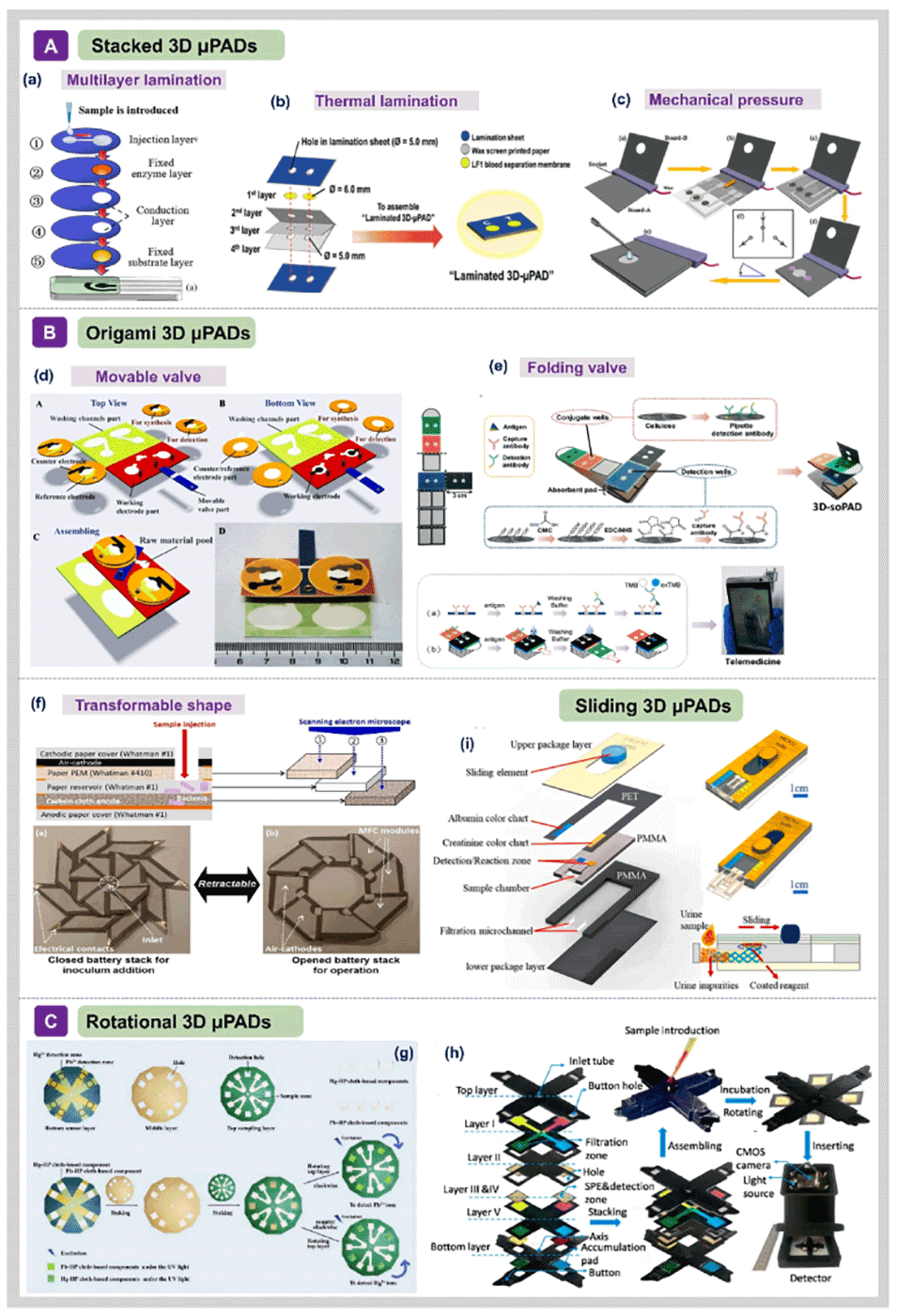
图6.多层3D μPAD的设计策略。
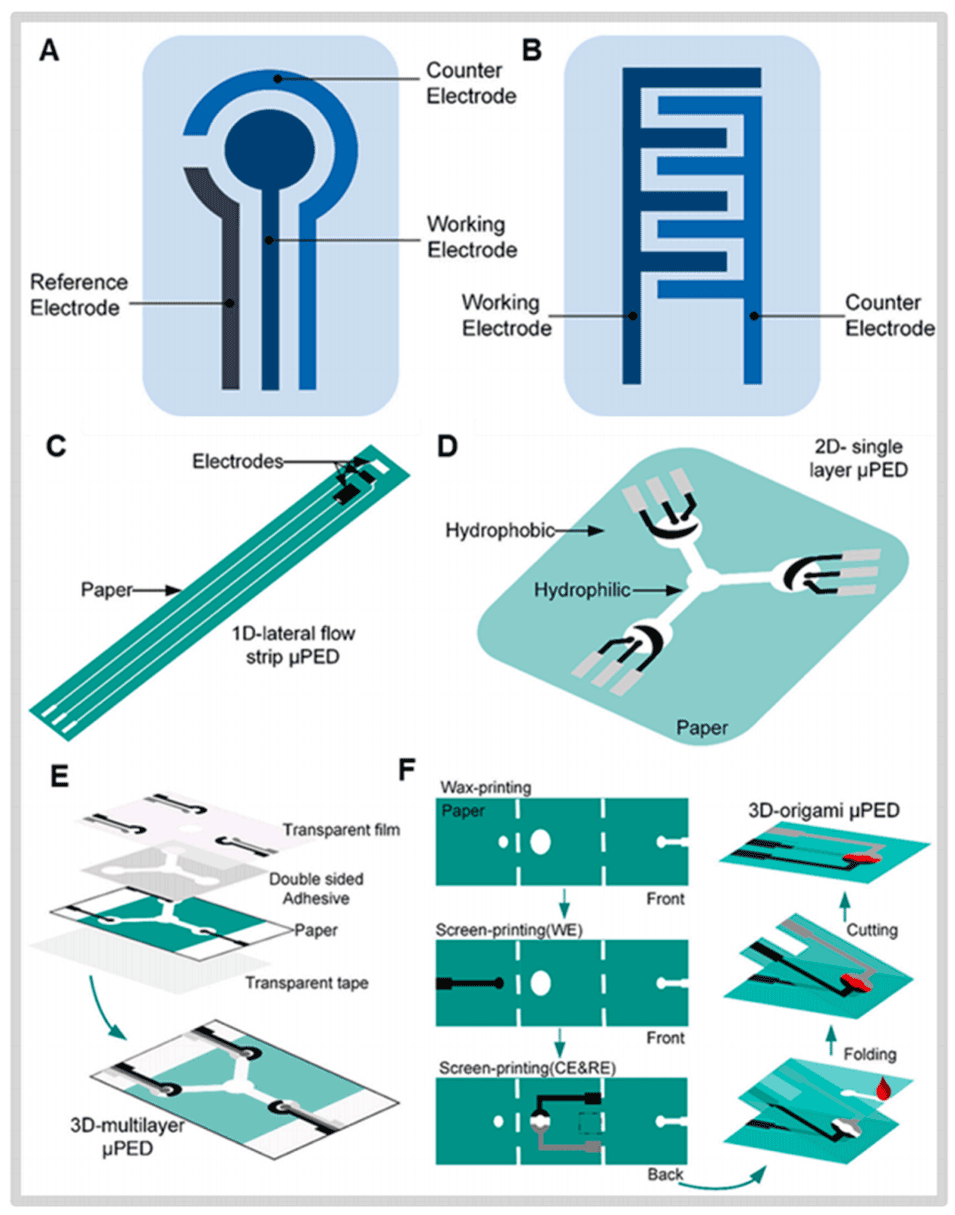
图7.(A)三电极系统和(B)两电极系统的最佳表面积图案。(C)具有三电极电化学的1D LFA;(D)具有三电极系统的2D单层μPAD;(E)3D多层电化学μPAD;和(F)3D折纸电化学μPAD。
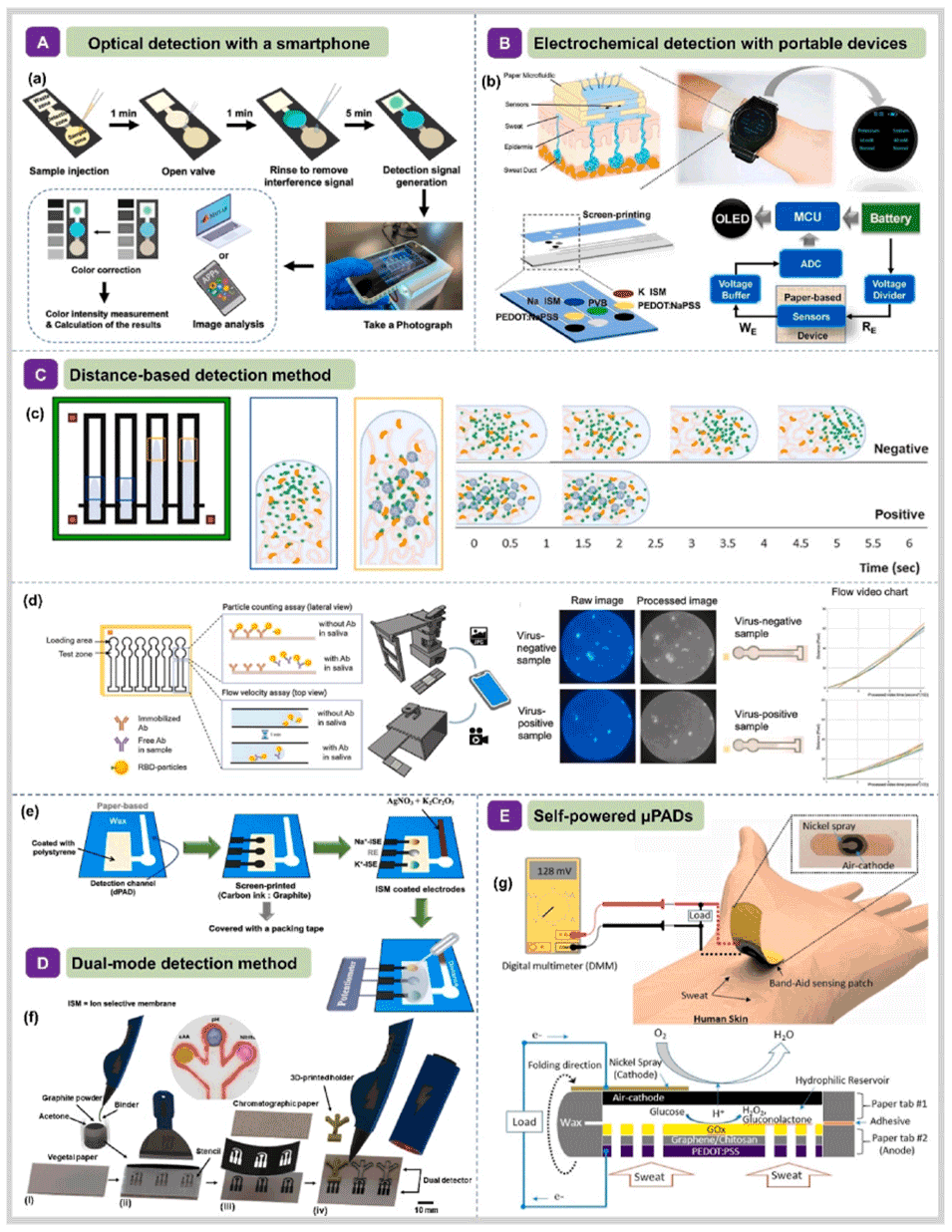
图8.(A)使用智能手机进行光学检测;(B)利用便携式微型设备进行电化学检测;(C)基于距离的检测方法;(D)双模式检测方法;(E)自供电μPAD。
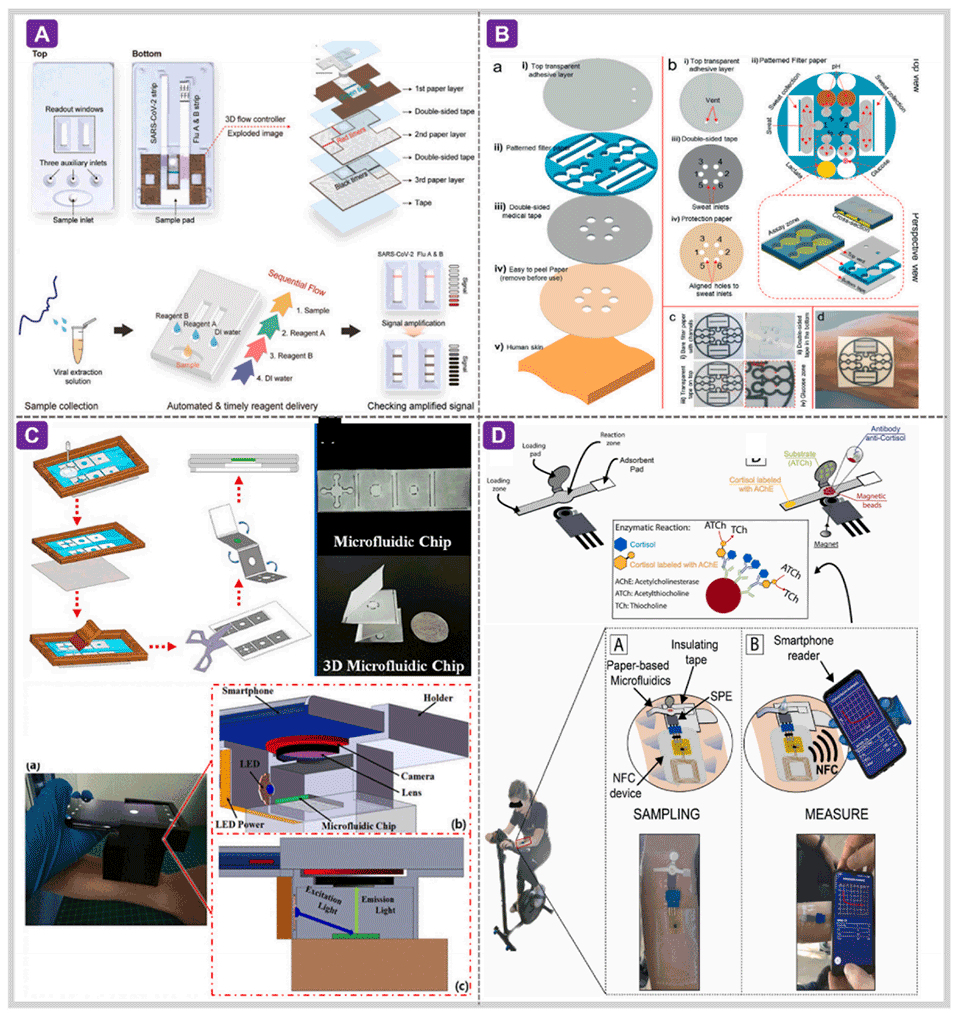
图9.用于无创检测的多维μPAD。
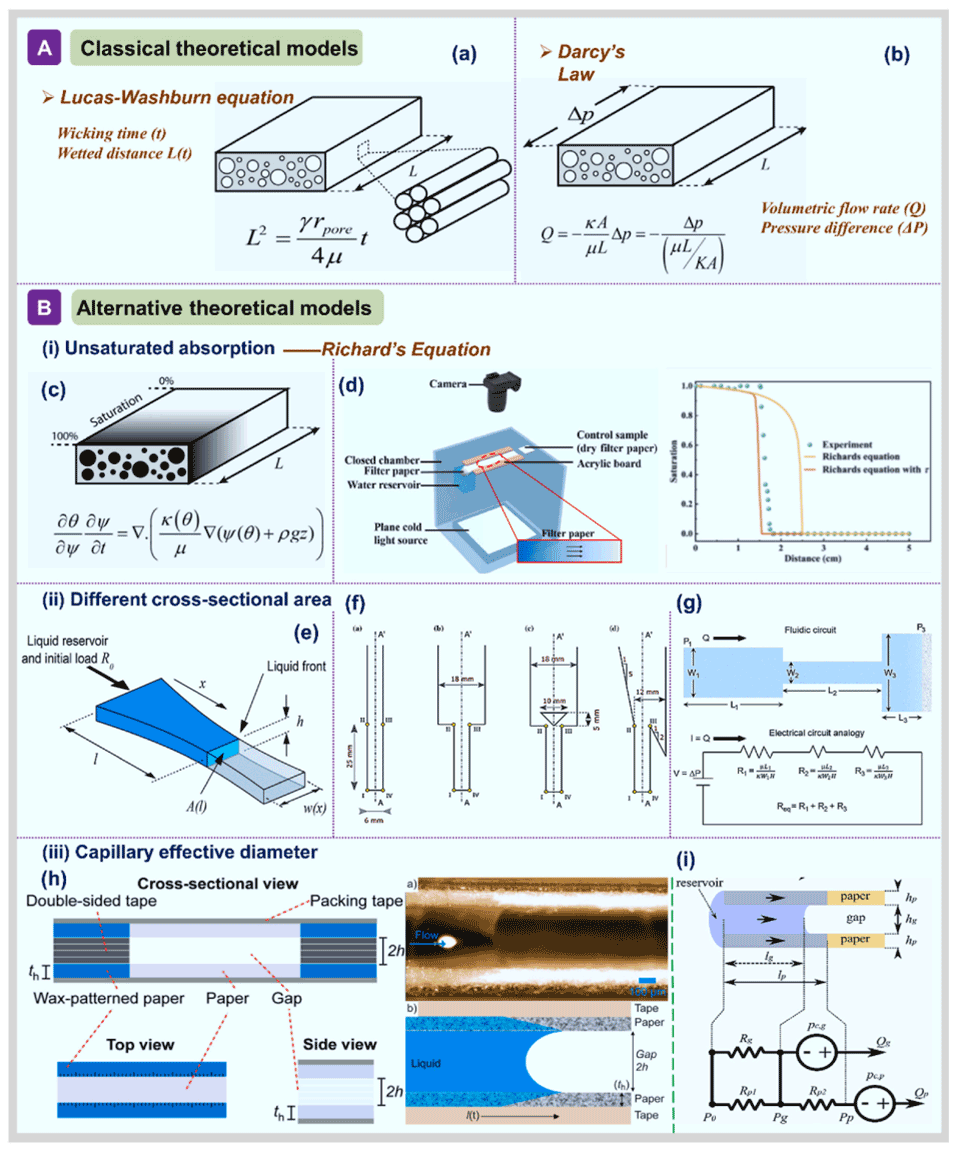
图10.(A)经典理论模型:(a)Lucas-Washburn方程,(c)达西定律;(B)替代理论模型:(c–d)不饱和吸收——Richard方程;(e–g)不同的横截面积。(h–i)毛细管有效直径。
原文链接:https://doi.org/10.1016/j.aca.2024.342877